
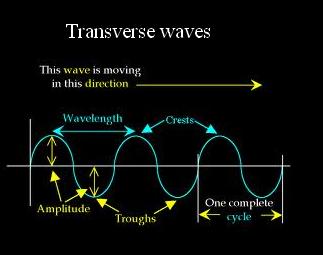
Values of the coefficient of friction between string and pulley, calculated from the amplitude of the pulley when rotation began, are in fair agreement with values which were found directly. Now study the lateral displacement of the string from the initial position. When it is plucked or bowed, progressive transverse waves move along. This vibrating string problem or wave equation has fixed ends at x 0 and x L and initial position, f(x), and initial velocity, g(x). One effect concerns the other transverse mode of the string. Values of the elastic modulus calculated from the lengths at which the rotation of the pulley reversed show a moderately good agreement with directly determined values. The state of the art of active control of moving strings is surveyed on controllability and observability, the Laplace transform domain analysis and the energy analysis, nonlinear vibration. The vibrations created by a string are nothing but a wave. Our simulation of the longitudinal string vibrations has omitted several important effects. The string used shows considerable elastic after effect, and its modulus of elasticity increases with the load. In experimental tests of the above theory, the senses of rotation observed for different lengths of the vertical part of the string agree with the theory in a great many cases, but differ in so many other cases as to show that the theory needs modification-probably by taking account of damping. transverse vibrations of a uniform stretched string form a suitable introduction to.
The theory indicates that the sense of the rotation depends on the length of the vertical part of the string, but is independent of the length of the horizontal part. 172 CHAPTER 4 THE TAUT STRING The philosophical theory of harmonics. Department of Mechanical and Aerospace Engineering, University of Miami, Coral Gables, Florida, USA. The notes and questions for Transverse Vibrations of Strings have been prepared according to the exam syllabus. It is shown that any slipping will first occur when the pulley is close to an end of its swing, and from this it follows that the sense of a net rotation is determined by the particular end of the swing at which this slipping occurs. String theory depicts strings of energy that vibrate, but the strings are so tiny that you never perceive the vibrations directly, only their consequences. The equations of motion are solved under the assumptions that there is no transverse vibration of the string, that the string does not slip on the pulley, that there is no damping, and that the motion is simple harmonic with a frequency equal to that of the tuning fork. The apparently continuous rotation which may sometimes be observed in the pulley in Melde's experiment is assumed to be the result of a succession of small slips of the pulley under the string near some particular phase of the motion.


 0 kommentar(er)
0 kommentar(er)
